I used the vector space model about a decade ago when I worked on the simple search engine for the company documents. Today the subject came up in the conversation and I was surprised as to how quickly I remembered this. I still think that this is rather elegant.
Tag: math
Guinness bubbles problem – solved!
If you are a beer fan, you’ve probably heard about the famous Guinness bubbles problem. While bubbles in most other beers rise up, in Guinness they go down. A lot of people were puzzled by that fact, and now, it seems, the puzzle is solved.
According to the article in Technology Reviews, Irish mathematicians came up with an answer:
Today, a dedicated team of Irish mathematicians reveal the answer. Eugene Benilov, Cathal Cummins and William Lee at the University of Limerick say the final piece in this puzzle is the shape of the glass, which has a crucial influence over the circulatory patterns in the liquid.
To understand how, first remember that the motion of every bubble exerts a drag on the liquid around it. Now imagine what would happen if there were a region of liquid containing fewer bubbles near the wall of a pint glass and consequently a region of higher bubble density near the middle of the glass.
Benilov and co say that the drag will be higher in the region where the bubble density is higher, in other words near the centre of the glass. This creates an imbalance that sets up a circulation pattern in which the liquid flows upwards in the centre of the glass and downwards near the walls.
That’s exactly as observed in a pint of Guinness.
There are more details and image of an anti-pint in the article. Read it.
Also, while reading up on the subject, I’ve learned something else about Guinness – the widget.
Statistics in a time of war
John D. Cook shares this interesting piece of history:
During WWII, statistician Abraham Wald was asked to help the British decide where to add armor to their bombers. After analyzing the records, he recommended adding more armor to the places where there was no damage!
This seems backward at first, but Wald realized his data came from bombers that survived. That is, the British were only able to analyze the bombers that returned to England; those that were shot down over enemy territory were not part of their sample. These bombers’ wounds showed where they could afford to be hit. Said another way, the undamaged areas on the survivors showed where the lost planes must have been hit because the planes hit in those areas did not return from their missions.
Wald assumed that the bullets were fired randomly, that no one could accurately aim for a particular part of the bomber. Instead they aimed in the general direction of the plane and sometimes got lucky.
It stories like this one, of a practical application, that make me regret of being a bad student. I think that more of these should be a part of a curriculum.
Bayes theorem history
A fascinating read on the Bayes theorem history:
The German codes, produced by Enigma machines with customizable wheel positions that allowed the codes to be changed rapidly, were considered unbreakable, so nobody was working on them. This attracted Alan Turing to the problem, because he liked solitude. He built a machine that could test different code possibilities, but it was slow. The machine might need four days to test all 336 wheel positions on a particular Enigma code. Until more machines could be built, Turing had to find a way for reducing the burden on the machine.
He used a Bayesian system to guess the letters in an Enigma message, and add more clues as they arrived with new data. With this method he could reduce the number of wheel settings to be tested by his machine from 336 to as few as 18. But soon, Turing realized that he couldn’t compare the probabilities of his hunches without a standard unit of measurement. So, he invented the ‘ban’, defined as “about the smallest change in weight of evidence that is directly perceptible to human intuition.” This unit turned out to be very similar to the bit, the measure of information discovered using Bayes’ Theorem while working for Bell Telephone.
If the whole thing is too much for you, at least read the “Bayes at War” section.
Learning about Markov chain
I’ve been hearing about “Markov chain” for long enough – it was time I learned something. Wikipedia seemed like a good starting point. I have to warn you though, be careful with scrolling on that page, because you can easily end up looking at something like this:
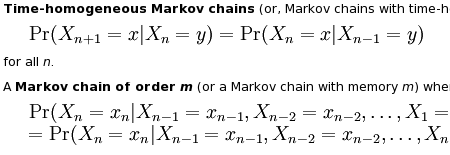
If you aren’t a rocket scientist or someone who solves integrals for fun, by all means, use the contents menu or jump directly to the Applications section.That’s where all the fun is. Here are some quotes for you to get interested and for me to remember.
Physics:
Markovian systems appear extensively in physics, particularly statistical mechanics, whenever probabilities are used to represent unknown or unmodelled details of the system, if it can be assumed that the dynamics are time-invariant, and that no relevant history need be considered which is not already included in the state description.
Testing:
Several theorists have proposed the idea of the Markov chain statistical test, a method of conjoining Markov chains to form a ‘Markov blanket’, arranging these chains in several recursive layers (‘wafering’) and producing more efficient test sets — samples — as a replacement for exhaustive testing.
Queuing theory:
Claude Shannon’s famous 1948 paper A mathematical theory of communication, which at a single step created the field of information theory, opens by introducing the concept of entropy through Markov modeling of the English language. Such idealised models can capture many of the statistical regularities of systems. Even without describing the full structure of the system perfectly, such signal models can make possible very effective data compression through entropy coding techniques such as arithmetic coding. They also allow effective state estimation and pattern recognition
Internet applications:
The PageRank of a webpage as used by Google is defined by a Markov chain.
and
Markov models have also been used to analyze web navigation behavior of users. A user’s web link transition on a particular website can be modeled using first or second order Markov models and can be used to make predictions regarding future navigation and to personalize the web page for an individual user.
Statistical:
Markov chain methods have also become very important for generating sequences of random numbers to accurately reflect very complicated desired probability distributions – a process called Markov chain Monte Carlo or MCMC for short. In recent years this has revolutionised the practicability of Bayesian inference methods.
Gambling:
Markov chains can be used to model many games of chance. The children’s games Snakes and Ladders, Candy Land, and “Hi Ho! Cherry-O”, for example, are represented exactly by Markov chains. At each turn, the player starts in a given state (on a given square) and from there has fixed odds of moving to certain other states (squares).
Music:
Markov chains are employed in algorithmic music composition, particularly in software programs such as CSound or Max. In a first-order chain, the states of the system become note or pitch values, and a probability vector for each note is constructed, completing a transition probability matrix
Markov parody generators:
Markov processes can also be used to generate superficially “real-looking” text given a sample document: they are used in a variety of recreational “parody generator” software
Markov chains for spammers and black hat SEO:
Since a Markov chain can be used to generate real looking text, spam websites without content use Markov-generated text to give illusion of having content.
This is one of those topics that makes me feel sorry for sucking at math so badly. Is there a “Markov chain for Dummies” book somewhere? I haven’t found one yet, but Google provides quite a few results for “markov chain” query.
